在鏈結串列實作的一開始，我覺得這題最合適：
Design Linked List
如題目的名字，就是讓我們自己去實現一個鏈結串列，不限定使用單向或雙向。
包含幾個方法

• MyLinkedList()：建構一個新的 Linked List 物件
• int get(int index)：如果鏈結串列中存在第 index 個元素，返回該值
• void addAtHead(int val)：新增一個數值為 val 的節點在鏈結串列的最前頭
• void addAtTail(int val)：新增一個數值為 val 的節點在鏈結串列的最後
• void addAtIndex(int index, int val)：如果鏈結串列中存在第 index 個元素，在該位置後面插入一個新的節點，數值為 val
• void deleteAtIndex(int index)：如果鏈結串列中存在第 index 個元素，刪除該元素

在題目的限制上 index 一定會給至少為 0，所以在處理 index 是否合法的時候只要考慮大小，不用考慮負向值。
在結構設計上，我們可以維護一個總是指向鏈結串列頭節點的虛擬頭節點 _beforeHead ，同時維護一個 _size 來便於我們判斷 index 是否合法，避免每次判斷 index 的合法性都需要做遍歷。
題目中的兩個方法：addAtHead 和 addAtTail 實際上可以用 addAtIndex 來處理，addAtHead(val) = addAtIndex(0,val)，addAtTail(val) = addAtIndex(_size,val)，新增節點的方法哩，我們只要專注處理 addAtIndex 就可以了。

public class MyLinkedList {
    public int _size;
    public ListNode _beforeHead;

    public class ListNode{
        public int val;
        public ListNode next;
        public ListNode(int val){
            this.val = val;
        }
    }
    
    public MyLinkedList() {
        _size = 0;
        _beforeHead = new ListNode(-1);
    }
    
    public int Get(int index) {
        if(index >= _size){
            return -1;
        }
        var node = _beforeHead.next;
        var cnt = 0;
        while(cnt != index){            
            cnt++;
            node = node.next;
        }        
        return node.val;
    }
    
    public void AddAtHead(int val) {
        AddAtIndex(0, val);
    }
    
    public void AddAtTail(int val) {
        AddAtIndex(_size, val);
    }
    
    public void AddAtIndex(int index, int val) {
        if(_size < index){
            return;
        }
        var node = _beforeHead;
        var cnt = -1;
        while(cnt != index-1){
            node = node.next;
            cnt++;
        }
        var newNode = new ListNode(val);
        if(node.next != null){
            newNode.next = node.next;
        }
        node.next = newNode;
        if(index == 0){
            _beforeHead.next = newNode;
        }
        _size++;
    }
    
    public void DeleteAtIndex(int index) {
        if(_size <= index){
            return;
        }
        var cnt = -1;
        var node = _beforeHead;
        while(cnt != index-1){
            cnt++;
            node = node.next;
        }
        node.next = node.next.next;
        _size--;
    }
}

這題可以寫得很有把握的話，大致上關於鏈結串列的結構認識跟操作就可以了。
接下來讓我們先來看一下昨天提到鏈結串列反轉的部分，雙指針的部分會在後面討論環的時候用到，

反轉單向鏈結串列

我們再在這邊重新定義一次，反轉鏈結串列的方法我們的預期是給入一個節點，將該節點到與該節點所在的鏈結串列的尾端為止全部節點順序翻轉。

迴圈

寫迴圈的話先把每次迴圈要做的事直觀的列下來，是開始寫迴圈的第一步。
假設現在 1->2->3->4->5 這個鏈結串列，第一步從頭開始遍歷，我們應該先處理 1->2這個片段(反轉後預期為 2->1)，要做的事有：

1. 記住 1 指向的節點
2. 把 1 指向的節點指向 1
3. 把 1 指向上一個節點
4. 處理完片段，把 1 存到上一個節點的位置，讓下一個節點可以指向 1
5. 接著回到步驟 1，往下一個節點處理
   所以 1->2 實際上跑完一次上面的步驟後，會處理完 1 指向 Null、2 指向 1，把 2 當作下一個處理節點，遍歷到鏈結串列的尾端。
   看完步驟，迴圈的程式碼也就寫完了，就是把上面的敘述翻成程式碼而已。

public class Solution {
    public ListNode ReverseList(ListNode head) {
        ListNode last = null;
        while(head != null && head.next != null){
            var temp = head.next;
            head.next = last;
            last = head;
            head = temp; 
        }

        if(head != null){
            head.next = last;
        }
        return head;
    }
}

迴圈是相對直觀的，對鏈結串列的結構有點概念即使是第一次要寫出來應該也沒問什麼問題。
畢竟迴圈是線性思考，和人腦的思考方式一樣，再來我們來看看遞迴怎麼寫。

遞迴

要寫遞迴先跳出程式碼，思考兩件事：

1. 我們要另外定義一個函式跑遞迴嗎
2. 就題目的題意來說，執行遞迴的函式期望得到的結果是什麼
   以這題而言，我們先嘗試在這個 ReverseList 函示直接當作遞迴本體來寫。
   而這個函式預期解決的問題是：「給予一個頭節點，反轉從這個頭節點以後的所有節點，並且預期會回傳反轉後的新頭節點」
   釐清函式定義，我們才能夠決定什麼時候要開始呼叫函式。

以下是遞迴反轉的步驟，可以看完步驟嘗試寫寫看。
1.首先定義終止條件：當給予的節點為空、或是給予的節點下一個為空(只有一個節點)的情況，無須再做任何反轉，直接回傳傳進來的節點
2.假設我們目前有 1->2->3->4->5，我們丟入 1 的時後，如果在 1 執行的過程，開始遞迴，再丟入 1 的後面，我們預期回傳回來的應該是 5->4->3->2 已反轉的鏈結串列，且回傳回來的節點應該是反轉後的新頭節點，也就是 5
3.所以我們可以透過呼叫函式得到節點 5 並反轉後面的所有節點順序，接著因為 1 自身完全還沒修改過，把 1 自己本來指向的 2 ，改成讓 2 指向 1(反轉)
4.因為 1 現在變成尾節點，再讓 1 指向 null
5.回傳 2. 步驟得到的節點 5，即為題目所求新的頭節點

再來來看程式碼。

public class Solution {
    public ListNode ReverseList(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
        var newHead = ReverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

遞迴的思考邏輯真的相對不直觀，在遞迴中最重要的就是終止條件，跟呼叫遞迴函式走一層的時機，以及函式回傳回來的定義，搞明白這幾個，才不容易被遞迴一層一層繞的頭暈。
如果沒有上面的步驟，直接看程式碼，可能還會有點不明所以，但有過說明後，相信應該能幫助大家理解遞迴的反轉鏈結串列的寫法原因。

有環無環 - 龜兔賽跑(Floyd Cycle Detection Algorithm)

最後昨天提到跟鏈結串列結構相關的問題，有環無環。
如昨天提到的環指的是鏈結串列透過單向移動，是否會移動到結尾節點，或是持續在串列內循環。
有個算法叫做 Floyd Cycle Detection Algorithm，通俗的名字叫做龜兔賽跑。
我們來看看這個算法能解決什麼樣的問題：
Linked List Cycle II
題目會給一個頭節點，我們要判斷該鏈結串列有沒有環，有環的話要回傳入口的 index(從0開始)，無環則回傳 -1。
題目寫了個二，就知道有一的版本，一是比較簡單一點的，只需要判斷有沒有環就好。

這邊之所以會叫做龜兔賽跑，其實就是雙指針出場的時候 ─ 快慢指針。
基本理論就是，如果我們讓兩個指針，一個指針每次走一步(烏龜)，另一個每次走兩步(兔子)，假設這是一個有環的路徑，則兔子必會從後面繞一圈追到烏龜；反之亦然，如果無環，則兔子會先遇到終點。
至此，題目一的版本就解決了，上面的概念實現，並不難。

但題目二要我們找到入口節點，我們該怎麼找到入口節點呢？
首先，我們先想想，在有環結構裡，兔子會在哪追上烏龜呢？有環結構表示前面有一小段路(或沒有)，接著才是循環的環結構，兔子遇到烏龜的地方必然是在環中 ─ 因為在無環的地方，烏龜走得比較慢，一定碰不上兔子，兔子會碰到烏龜，是因為兔子已經跑完一圈了。假設相遇時烏龜走了 k 步，兔子相對的就走了 2k 步。
兔子跟烏龜差了 k 步，這個差的 k 步必然等於環的長度的倍數，這樣他們才能夠相遇。
相遇的點假設是進環後 m 步的位置，則環的起點到環入口點距離為 k - m(烏龜走的步數減去進環後的位置)。
相遇表示兔子至少繞了環一圈，我們假設就正好繞了一圈後相遇，則從相遇點走到環入口的位置也會為 k - m。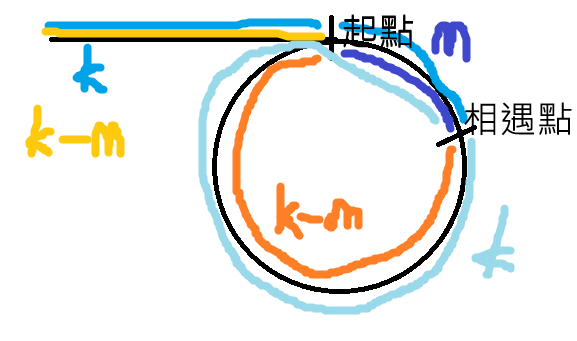

覺得文字抽象的話，可以配合著圖看，應該就會清楚了，這邊最重要的是我們發現了兩個 k - m。
意思是什麼？知道相遇的點後，只要我們同時有另一個新的指標，兩個指標每次都走一步，相遇的地方，就會是入口的地方。
知道上面這個原理推論後，我們就可以動手了。

public class Solution {
    public ListNode DetectCycle(ListNode head) {
        var slow = head;
        var quick = head;
        if(head == null || head.next == null) return null;
        while(slow != null && quick != null){
            slow = slow.next;
            quick = quick.next;
            if(quick.next!=null){
                quick = quick.next;
            }
            if(slow == quick){
                slow = head;
                while(slow!=quick){
                    slow = slow.next;
                    quick = quick.next;
                }
                return slow;
            }
        }
        return null;
    }
}

slow 代表的是龜(走得慢的)，quick 代表的是兔(兩倍速)，基本就是按照上面描述的邏輯實作。
建議看完覺得懂了之後，另外重新自己推導一次上面的過程，確定至少現在這個時刻是懂得，看著覺得講得明白，換自己重新想一次可能就會發現有細節沒有理解清楚。
自己動手才能夠確信自己懂了。

鏈結串列結構相關的題目跟特性大概到這裡，下篇我們會來探討關於雜湊表。